Aufgabe
Von einem quadratischen Pyramidenstumpf sind gegeben (in cm):
a = 8, b = 6, h = 5,
gesucht sind:
a) Höhe h* der Ergänzungspyramide,
b) Inhalt der Trapezseitenfläche,
c) Volumen des Pyramidenstumpfs,
d) Bestimmen Sie den kürzesten Weg auf der Pyramidenstumpfoberfläche zwischen A und G
Lösung:
a) h* ÷ b= (h*+h)÷ a
h*a = h*·b + h·b
h* = h·b ÷ {a-b} = 5· 6 ÷ 2 = 15
b) hs = √ 5 2 + 1 2 = √ 26 = = 5,09901951359
A = 7√26 =35,693136
c) V =⅓· 5 (64 + 48+ 36) = 246,66666666
d) Seitenkante: s = √{25+ 2} = 5,1961524227066318805823390245176
d= 6 √2 = 8,4852813742385702928101323452582
stot = 13,6819 13.12 14.56
Aufgabe
Eine Öllampe hat die Form einer geraden Pyramide mit quadratischer Grundfläche. Die Innenmaße der Pyramide sind: Höhe h = 10 cm und Grundkante a = 6 cm.
a) Wie viele ml Öl kann man maximal in die Lampe einfüllen?
b) Wie viel Öl befindet sich in der Lampe, wenn das Öl im Innern bis 1 cm über dem Boden steht?
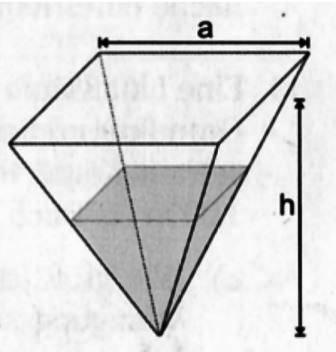
c) Zum Nachfüllen von Öl muss man die Lampe so umdrehen, dass die Spitze nach unten weist (siehe Abbildung). Wie hoch steht nun das Öl in der Lampe, wenn man die Füllmenge von b) annimmt?
Lösung:
a) V0 = ⅓·6²·10 = 120 cm³
b) V = 120(1-0.9³ ) = 32.25 cm³
c) h÷a = 10 ÷ 6
V = ⅓·h (0.6 h)²
32.25 = ⅓·h (0.6 h)² → h = 6.453