Lineare Gleichungen mit einer Unbekannten

0=a·x + b →x = -b/a

a = 0→keine Lineare Gleichung

Aufgabe 1

Berechnen Sie die Lösung für x in G = R, mit Fallunterscheidung für alle Parameterwerte p.

(p - 4) · x = 16 - p²

Lösung:

a) x = (16 - p²)÷(p - 4) = -p-4

p≠4: x= - p - 4 oder L = { - p - 4}

p=4: L= G

Aufgabe 2

Berechnen Sie die Lösung für x in G = R, mit Fallunterscheidung für alle Parameterwerte p.

p² · x = p - 3 + p · x+ 6 x

Lösung:

x = (p-3)/(p²- p - 6) =1÷( p+2)

p=+3:                       L = G

p = -2:                     L = { }

p≠3 und p≠ - 2 :     x = 1÷{p + 2} oder L = {1÷(p + 2)}

Aufgabe 3

Die ersten beiden Waagen befinden sich im Gleichgewicht.

Wie viele rote Kugeln halten die grüne Kugel im Gleichgewicht?

Aufgabe

Die beiden Waagen sind im Gleichgewicht.

Was muss auf die rechte Waagschale gelegt werden, damit die Waage im Gleichgewicht ist?

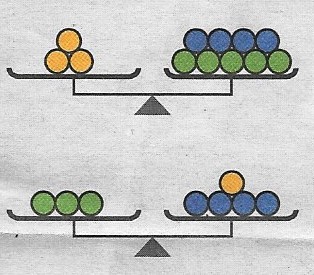
Lösung:    1 gelbe Kugel entspricht 2 grünen Kugeln

Aufgabe 4

Wunschgewicht
Wie kann man mit einer Balkenwaage exakt 2017 Gramm Pulver wägen?
Folgende acht Gewichtsteine stehen dabei zur Verfügung: 

1 g, 3 g, 27 g, 81 g, 243 g; 729 g und 2187 g.

Um beispielsweise 20 g abzuwägen legt man die beiden Steine 3 g sowie 27 g auf die eine Waagschale und auf die andere, wo auch das Pulver P draufkommt, 1 g sowie 9 g. Dann schüttet man solange Pulver auf die Waagschale, bis die Waage im Gleichgewicht ist.

Aufgabe 

Die beiden Waagen sind im Gleichgewicht.

Was muss auf die rechte Waagschale gelegt werden, damit die Waage im Gleichgewicht ist?  

Textaufgaben Geschwindigkeit Lineare Gleichungen

Aufgabe 5

Ein Fahrzeug fährt mit 6 km/h bergauf und anschliessend mit 18 km/h bergab. Für den gesamten Weg von 40 km benötigt es

3 h . Wann und wo erreicht es den höchsten Punkt?

Lösung:     6 x + ( 3 – x ) 18 = 40 → x = 7÷6 h = 70 min → s = 7÷6 h · 6 km/h = 7 km

Textaufgaben Zahlenrätsel  Lineare Gleichungen 

Aufgabe 6

Die Differenz der Quadrate von zwei natürlichen Zahlen mit dem Unterschied 3 beträgt 381. Wie heisst die kleinere der beiden Zahlen?

Lösung:    (x + 3)² – x² = 381 → x = 62

Aufgabe 7

Bestimmen Sie x.

a) 5 - x = 25 + 3 x – 4                                    Lösung:    x= -4

b) ( x + 3 )·( x – 5 ) = ( x – 3 )²                            Lösung:    x= 6

c) 2 ( a x – b x ) = x – 2 b x + c                     Lösung:    x = c÷(2 a-1)

d) ( x + n )² = ( x – n )² + 10 n                         Lösung:   x= 2.5

e) ( x – 4 a )² - x ( x + b )=b ( 7 x + 16 b )     Lösung:    x = 2·(a-b)

Lineare Gleichungen mit Parametern, Fallunterscheidung

Aufgabe 8

( a – x )·(x - 2) – ( b – x )· ( x + 2) = 4 · ( x – b )

Lösung:

a ≠ b→x = 2  oder L = {2}

a = b→ L = G 

Aufgabe 9

(a - x) · b + (a - c - x)·(x - b) = x·(a - x)

Lösung:

c≠ 0→x = b oder L ={ b }

c = 0→L = G 

Aufgabe 10

(a + b)· (x - b) = a² – b²

Lösung:

a ≠ -b→x = a  oder L = {a}

a ≠ -b→L = G

Aufgabe 11

Ein Behälter wird durch eine Speiseleitung in 4 Stunden gefüllt und durch eine Entnahmeleitung in 6 Stunden geleert.

a) Wann ist der Behälter gefüllt, wenn beide Leitungen geöffnet sind und der Behälter bereits zu einem Drittel gefüllt ist?

b) Wie lange dauert eine ¾ Füllung, wenn die Speiseleitung 2 Stunden vor der Entnahmeleitung geöffnet wird und der Behälter bei Füllbeginn leer war?

Lösung:

a)

^t/₄ – ^t/₆ = ²/₃

3 t -2 t =8 t = 8 h

Füllzeit 8 h

b)    ¾ - 2 · ¼ = ¼

^t/₄ - ^t/₆ = ¼

3 t - 2 t = 3 t = 3 h

Fülleitung resamthat 5 h, Entnahmeleitung 2 h

Aufgabe 12

Der Stundenlohn eines Angestellten beträgt bei normaler Arbeitszeit Fr. 56.-. Wird die normale Arbeitszeit überschritten, so wird der Stundenlohn für die Überzeit erhöht.

Ein Angestellter bekam in einer Woche, in der er 50 Stunden arbeitete, Fr. 2935.- und in einer zweiten Woche bei einer Arbeitszeit von 57 Stunden Fr. 3516.- Lohn.

a) Wie gross ist die normale wöchentliche Arbeitszeit?

b) Wie hoch ist der Lohnzuschlag für Überstunden?

Lösung:

x: Normarbeitszeit

y: Überstundenlohn

56 x + ( 50 - x ) y = 2935

56 x + ( 57 - x ) y = 3516

7 y = 581         y = 83 (Überstundenlohn)

56 x + (50 - x ) 83 = 2935 50 cdot 83 -27 x = 2935 → x = 45 (Normarbeitszeit)

Aufgabe 13

Bestimmen Sie die Parameter a und b so, dass die lineare Gleichung die Lösung x = ½ und y = -5 besitzt.

        x + a y     = 1         (I)

        b x + 2 y = 4        (II)

Lösung:

½ – 5 a = 1     →      a = -0.1

½ b - 10 = 4     →     b = 28